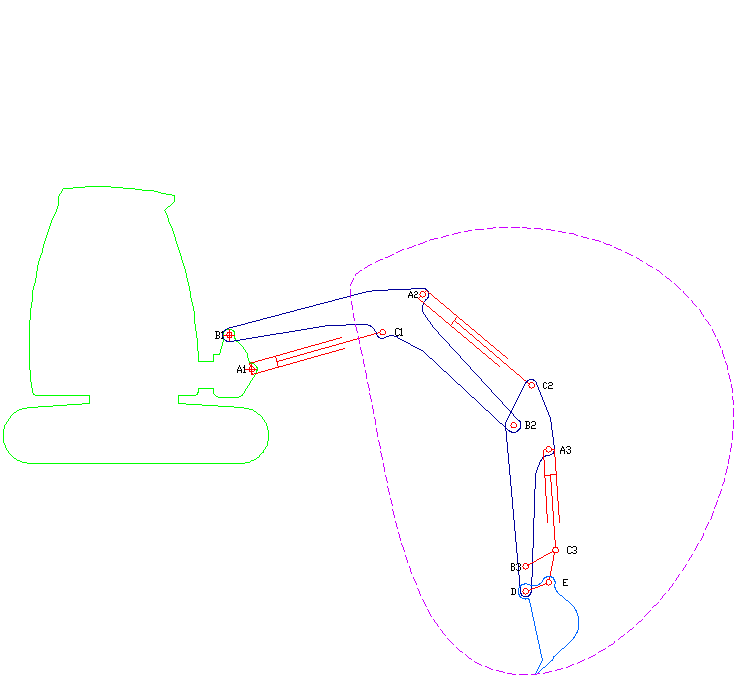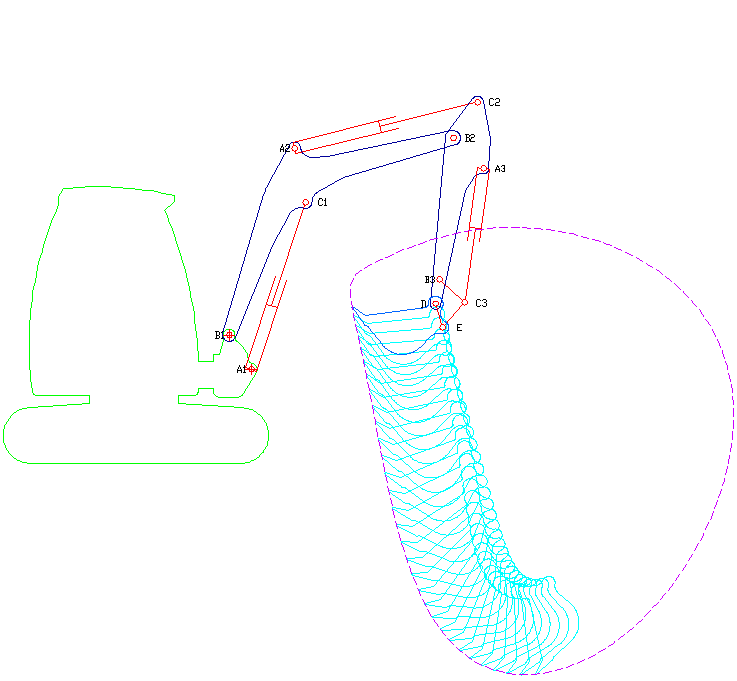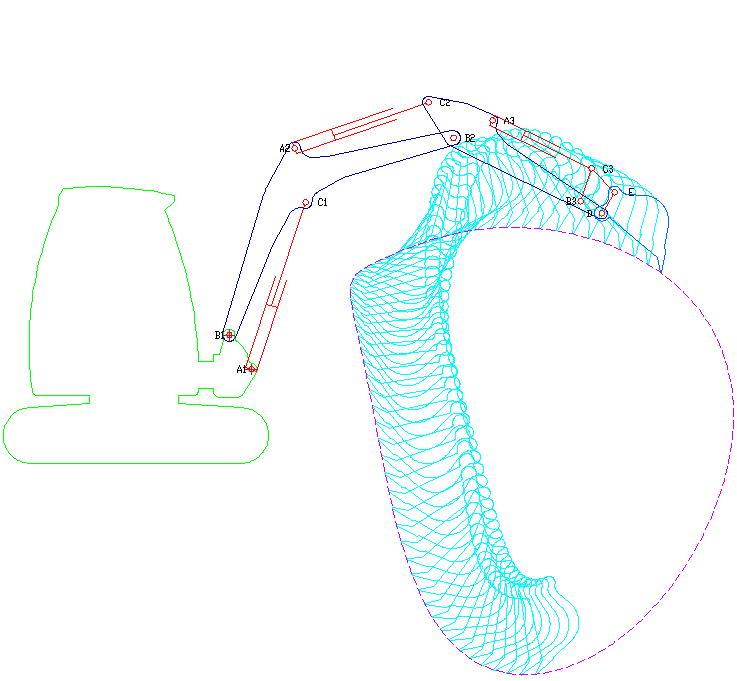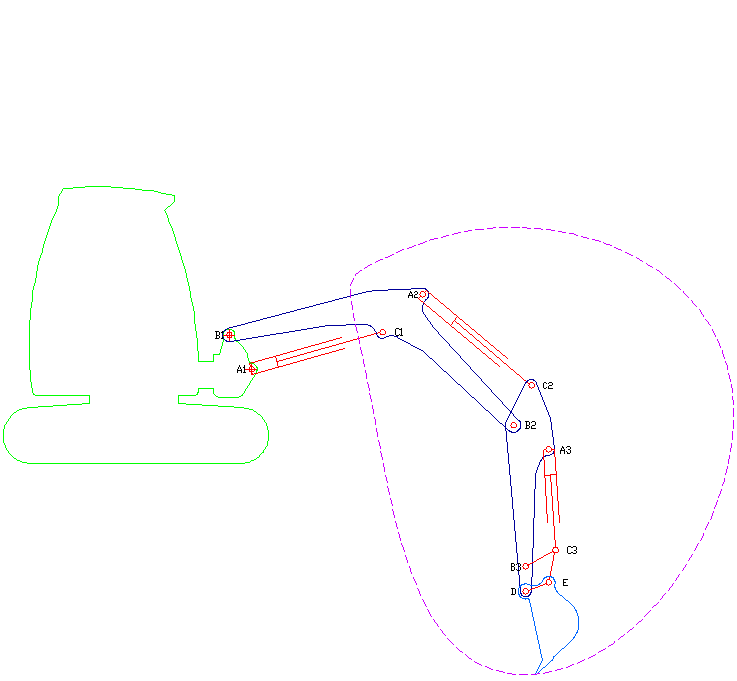
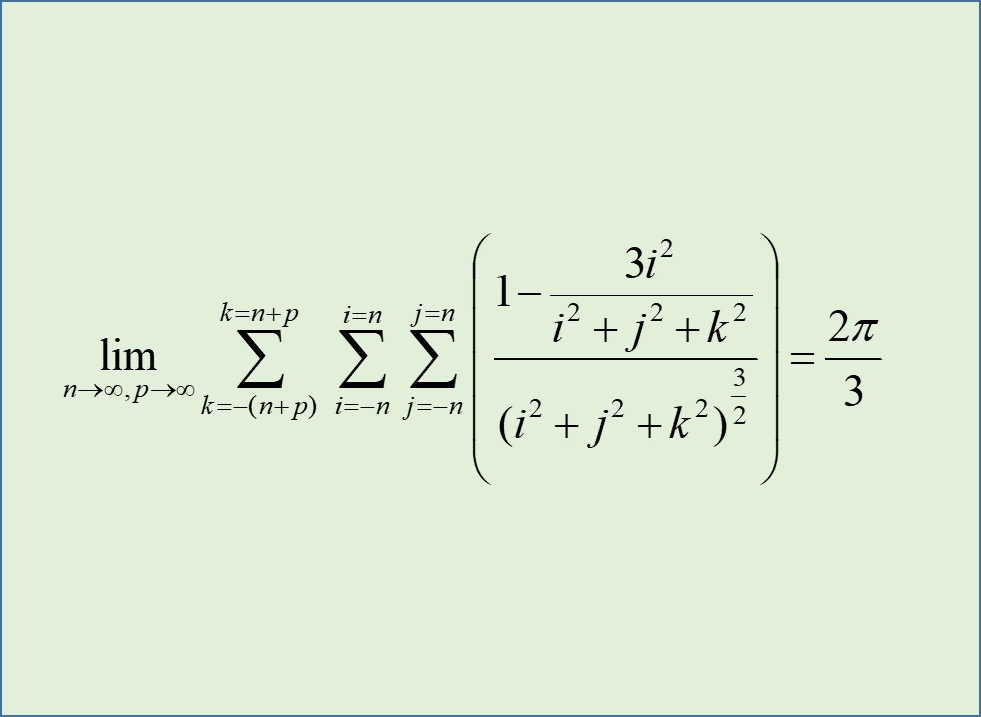ارسال شده توسط LesterFarley
شروع فعالیت 7 سال پیش
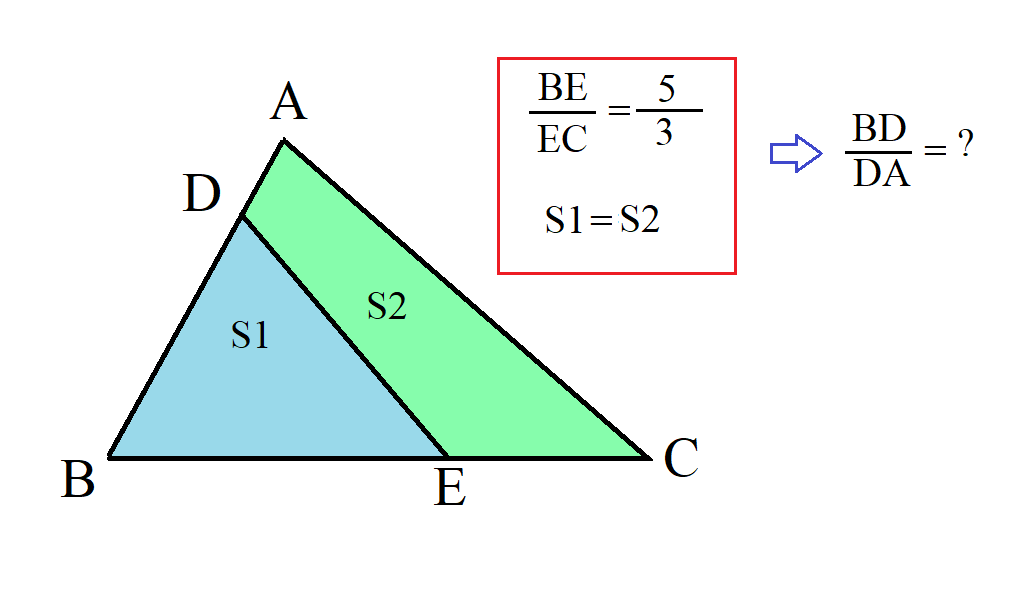
این سوال جالب و نسبتا ساده را در یک کتاب آمادگی آزمون ورودی یکی از مدارس راهنمایی خصوصی دیدم، یعنی دانش آموز کلاس ششم باید این را جواب بدهد. فکر میکنم برای دانش آموزان متوسط و حتی خوب سخت است.
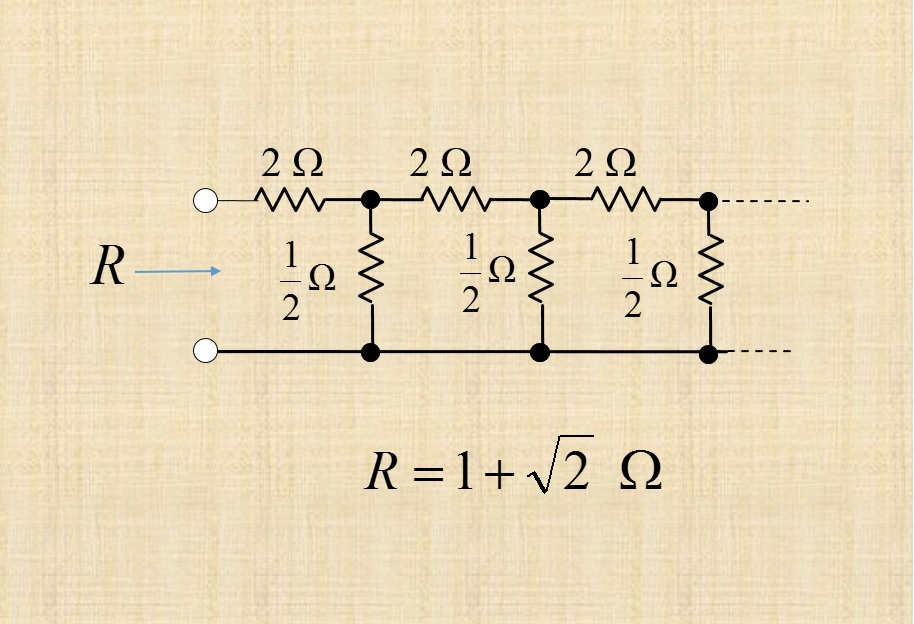
چند وقت پیش در حین انجام محاسباتی به این سری رسیدم. آن را جایی ندیده ام و میتوانم بگویم اوریجینال است، ولی یقین دارم ریاضی دانها و یا حد اقل فیزیکدانها با مفهوم آن آشنایند هر چند ممکن است به این صورت مطرح نکرده باشند. از آنجا که سری شامل سه مجموع است با دو حد بی نهایت است، اثبات ریاضی آن شاید دشوار باشد ولی با استفاده از قوانین الکترو مغناطیس نسبتا به راحتی اثبات میشود.
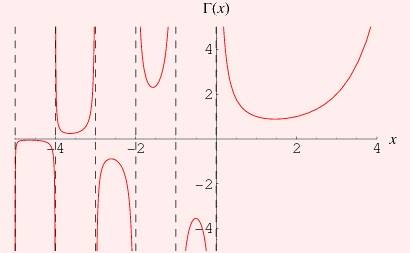
اگر نمودار یک تابع را قیافه آن تابع بدانیم، تابع گاما بد قیافه ترین تابعی است که تا کنون دیده ام. اگر تابعی قِناس تر از تابع گاما سراغ دارید لطفا معرفی کنید.
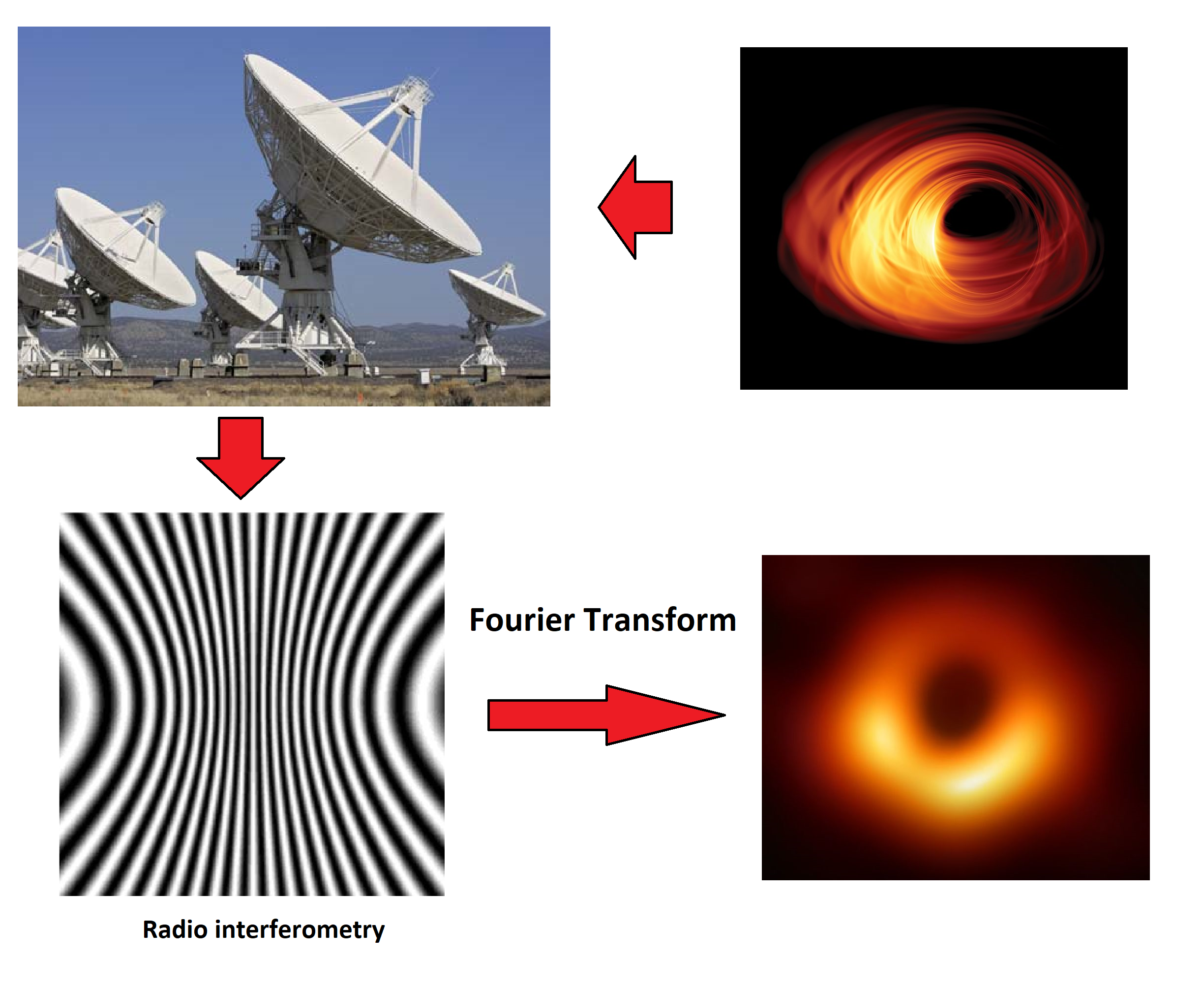
چندی پیش خبر تهیه اولین تصویر سیاهچاله در کانالهای خبری و شبکه های اجتماعی پیچید. این تصویر در واقع صحنه ۵۵ میلیون سال پیش است، چون آنقدر از ما دور است که ۵۵ میلیون سال طول کشیده است تا نور آن به ما برسد. ضمنا تصویر را از نور مرئی بدست نیاورده اند بلکه آن را از امواج رادیویی که از سیاهچاله رسیده است و با روش محاسباتی خاصی نتیجه گرفته اند. با اندکی ریاضیات میشود نشان داد که تصویر دو بعدی منبع امواج برابر است با تبدیل فوریه الگوی تداخل آن بر روی زمین.
خود سیاهچاله را نمیشود دید ولی با دریافت امواج الکترومغناطیسی اطراف آن میشود سیاهی اش را تشخیص داد. نزدیک ترین سیاهچاله مناسب برای رویت همین سیاهچاله M87 است که ۵۵ میلیون سال نوری از ما دور است. از خورشید ۲۷,۰۰۰ بار بزرگتر و میلیاردها بار سنگینتر است. قطر ظاهری آن در آسمانِ زمین به اندازه ای کوچک است که مثلا بخواهیم از روی قله دماوند تار مویی را در ساحل خلیج فارس در شهر بوشهر تشخیص دهیم. زاویه رویت این سیاهچاله نزدیک به یک «صد میلیونم» درجه است. قویترین تلسکوپ های نوری قدرت تشخیص چنین زاویه کوچکی را ندارند؛ به عنوان مثال قدرت تشخیص تلسکوپ Hubble یک «صد هزارم» درجه است. برای تشخیص M87 از روش تداخل امواج استفاده شده است که در آن لازم است از نقاط مختلف روی زمین تصویر رادیویی ثبت شود. هرچه فاصله نقاط بیشتر باشد اجسام دورتری را میتوان تشخیص داد، و هر چه تعداد نقاط بیشتر باشد کیفت تصویر بهتر است. تعداد ۸ تلسکوپ رادیویی در چند نقطه کره زمین نصب کرده اند که با چرخش کره زمین موقعیتشان نسبت به سیاه چاله تغییر کرده و تصاویر مستقل ثبت میکنند. هر تلسکوپ خود از ده ها و گاهی صدها آنتن تشکیل شده است. به مدت 8 ساعت تصاویر فراوانی از M87 تهیه کرده و سپس داده ها را با هواپیما به یک آزمایشگاه مرکزی حمل کردند. به علت حجم بسیار بالای داده ها، هواپیما بسیار زودتر از اینترنت آنها را به مقصد میرساند.در آزمایشگاه مرکزی با کمک یک کامپیوتر پرقدرت، تصاویر ثبت شده از ایستگاه های مختلف را همزمان کرده و سپس الگوی تداخل آنها را بدست آوردند. سپس با محاسبه تبدیل فوریه دو بعدی الگو ی تداخل، این شکل نه چندان واضح را بدست آوردند. با افزایش تعداد نقاط تصویر برداری و افزایش فاصله آنها میتوان تصویر واضح تری بدست آورد.
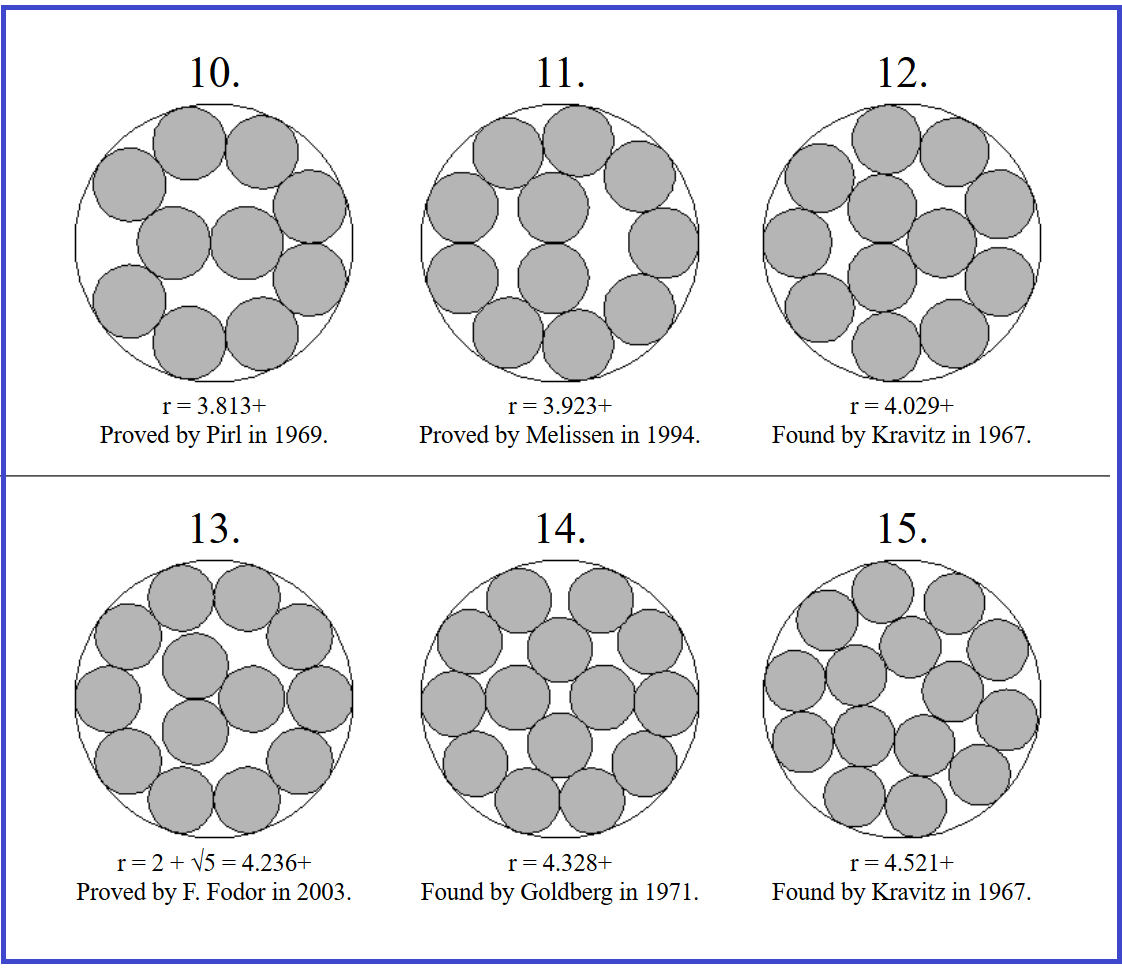
جاسازی بهینه n دایره در یک دایره، بطوری که فضای آزاد بین دایره ها کمترین باشد، یکی از مسائل رایج در ریاضیات کاربردی است. یافتن این چیدمانهای بهینه برای برخی از مقادیر n چندان هم ساده نیست. به عنوان مثال برای n=13، مساله تا سال 2003 حل نشده بود.
قطر دایره های کوچک در تصویر 1 است و قطر دایره دربرگیرنده هر گروه زیر آن نوشته شده است. مثلا میتوان 12 دایره به قطر واحد را در یک دایره به قطر 4.029 جا داد.
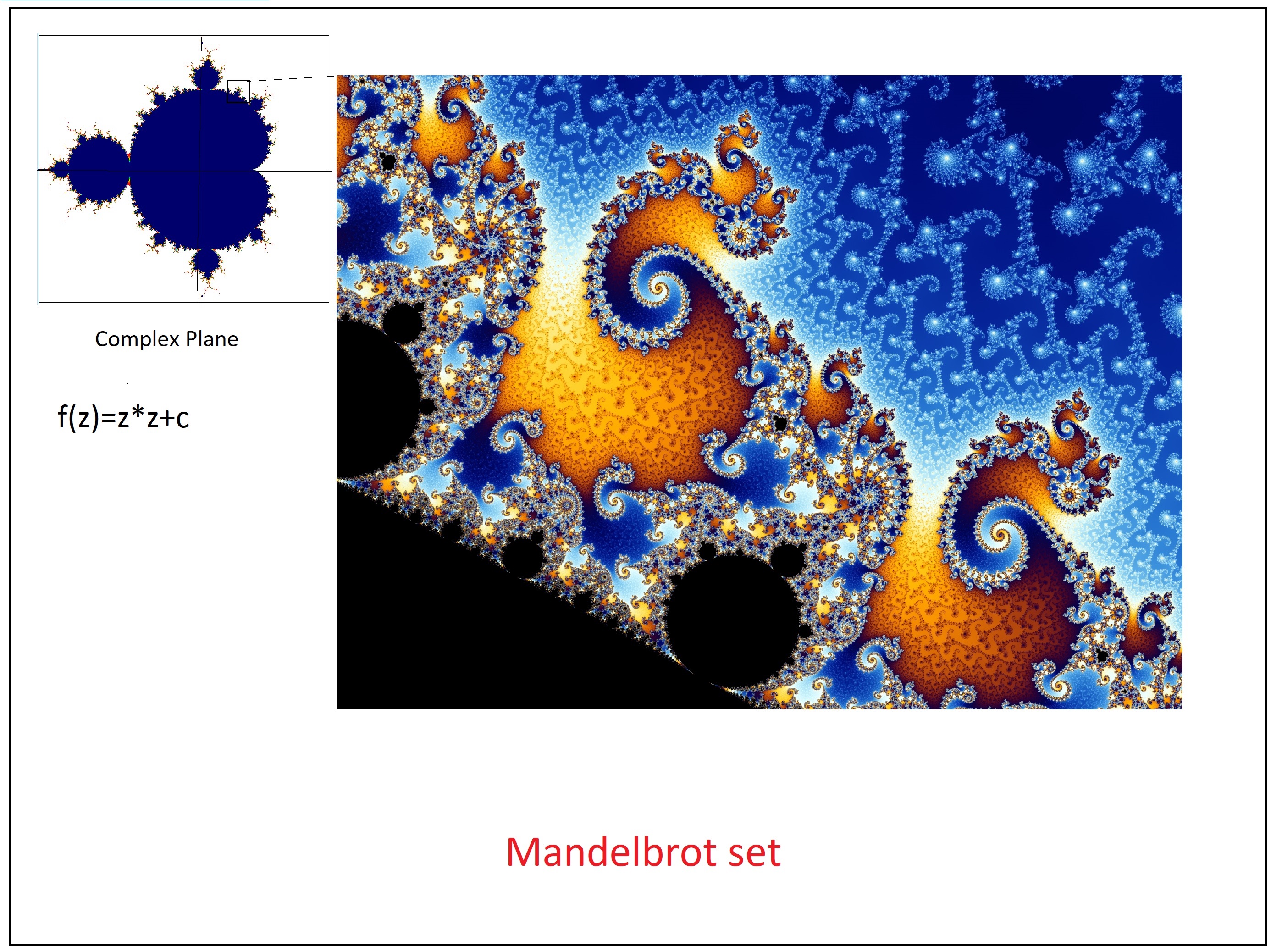
این نقاشی افسون کننده کار یک هنرمند نیست بلکه کار یک تابع مختلط است. این تابع برای هر نقطه از صفحه مختلط، یک سری اعداد طبیعی تولید میکند.با رنگ کردن هر نقطه بر اساس مقدار عدد آن، چنین تصویری بوجود می آید.
تابع مولد این مجموعه بسیار ساده است. برای عدد مختط z تابع f(z)=z*z+c را تعریف میکنیم که در آن c عددی ثابت است. آنگاه با شروع از نقطه اولیه z0 ، مجموعه ای از اعداد مختلف را اینگونه تولید میکنیم:
z1=f(z0)
z2=f(z1)
zk=f(zk-1)...zN=f(zN-1)
بعد از تولید هر نقطه، قدر مطلق آن را با ثابت R مقایسه میکنیم. اگر قدر مطلق zk از ثابت R بزرگتر و k کمتر از N باشد، به اصلاح میگویند نقطه گریخته است و در این صورت عدد k را به آن نقطه انتصاب میدهیم. اگر نقطه نگریزد عدد N را به آن نسبت میدهیم.
نقاط تاریک تصویر گریخته ها هستند. این مجموعه اعداد به N و دو ثابت R و c بستگی دارد.
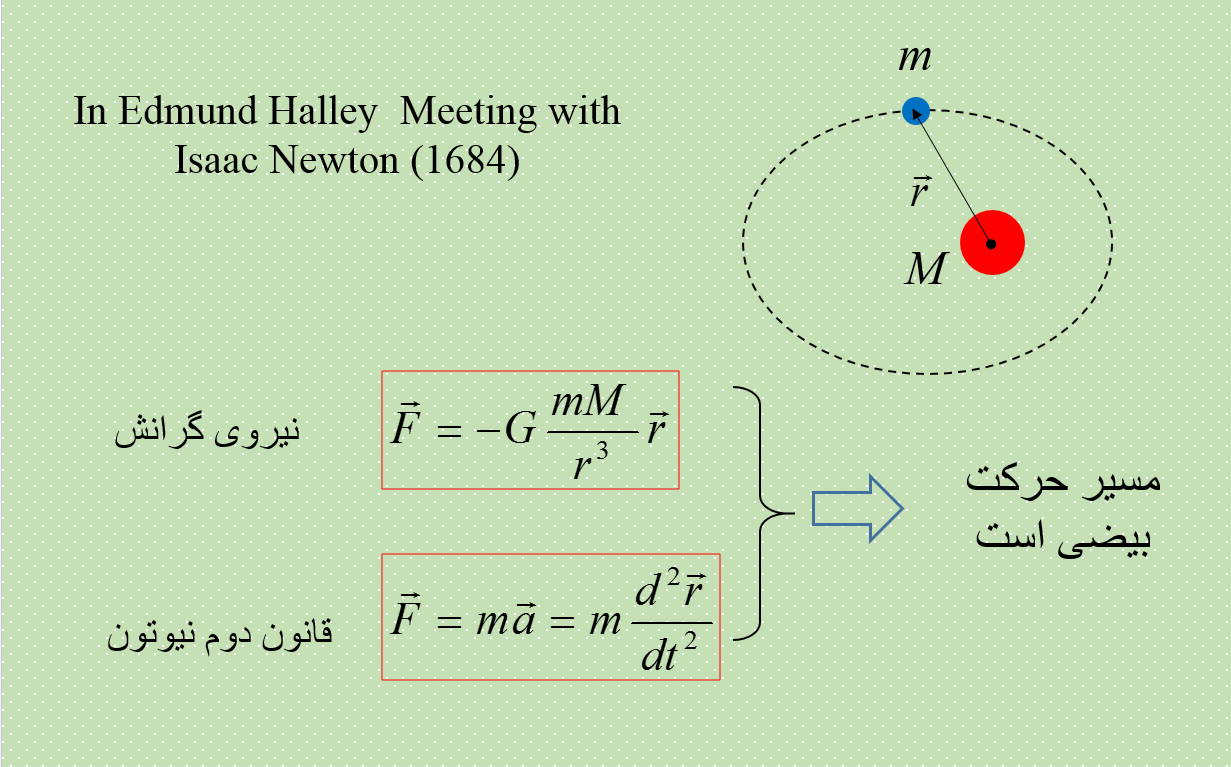
پیش از نیوتن، کپلر با اتکا به مشاهدات تجربی، چند قانون در مورد حرکت سیارات استخراج کرده بود. اولین قانون کپلر این است که مسیر حرکت سیارات به دور خورشید بیضی است و خورشید در یکی از این کانون های این بیضی قرار دارد.
نیوتون و با کشف مبانی ریاضی نیروی گرانش و قوانین مکانیک موفق شد قوانین کپلر را با روشهای ریاضی اثبات کند. در ملاقاتی که بین نیوتن و ادموند هالی رخ داد، نیوتن با اعتماد به نفس میگوید که مسیر حرکت سیارات به دور خورشید بیضوی است چون این را محاسبه کرده است. اما اثبات این ادعا به روش کاملا ریاضی سالها ریاضی دانان از جمله خود او را خسته کرد.
امروزه با پیشرفت هایی که در شاخه های معادلات دیفرانسیال و آنالیز برداری صورت گرفته است این اثبات نسبتا آسان است و تمرین خوبی است برای رسیدن به فهم عمیق تر این مباحث.
اطلاعات بیشتر حول این موضوع و همچنین اثبات امروزی ادعای نیتون را میتوانید در این لینک ببینید.
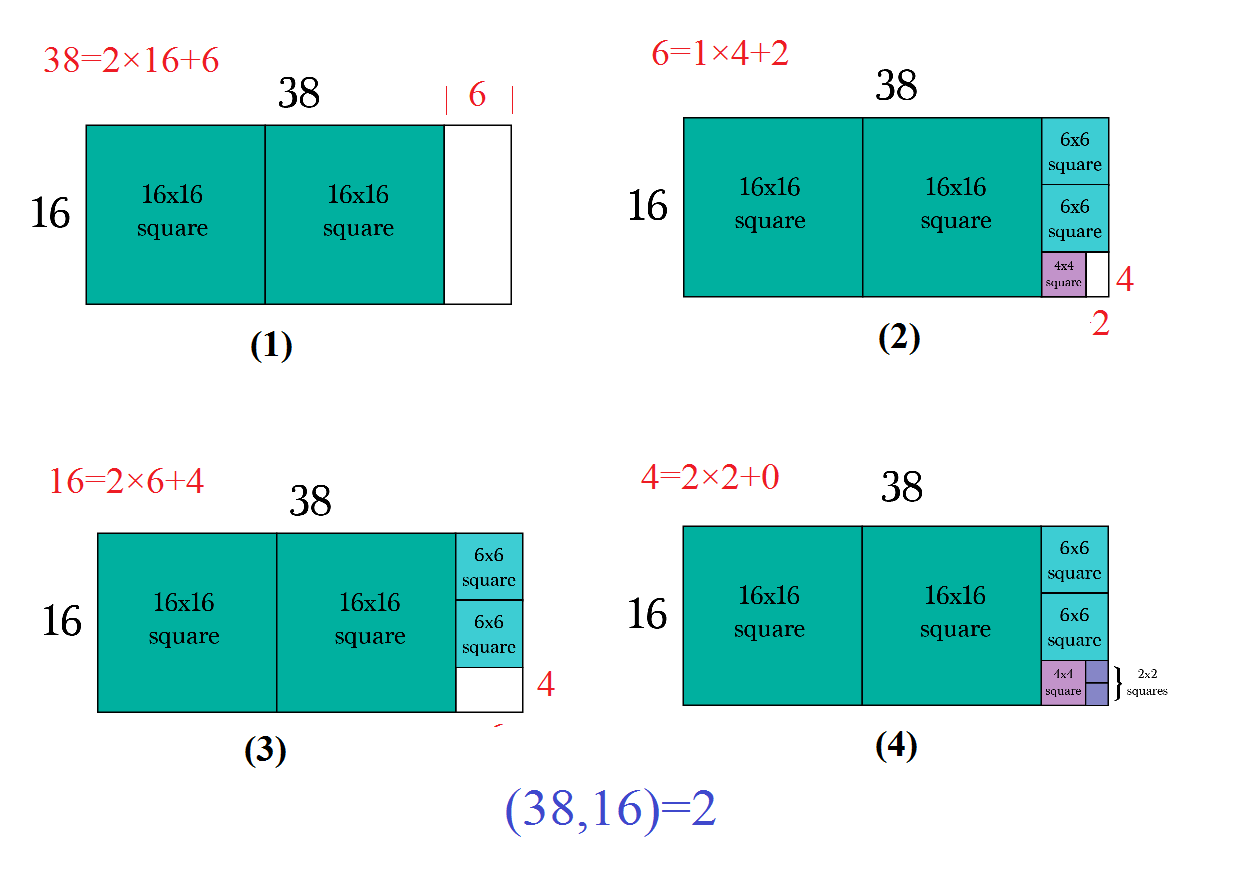
نمایش هندسی این الگوریتم در یکی از پست های گذشته آورده شد. این تصویر الگوریتم اقلیدس را به روش حسابی و با کمک کسرهای مسلسل شرح می دهد.
الگوریتمی که شرح آن در تصویر آمده است را با نام الگوریتم اقلیدس میشناسند. این الگوریتم بزرگترین مقسوم علیه مشترک دو عدد را پیدا میکند.
در این روش ابتدا مستطیلی با طولی و عرضی برابر با اعدادی که میخواهیم بزرگترین مقسوم علیه مشترک آنها را پیدا کنیم در نظر میگیریم و سپس تلاش میکنیم تا شکل را با بزرگترین مربعهای ممکن پوشش دهیم.
بزرگترین مقسوم علیه مشترک دو عد برابر با اندازه آخرین مربع خواهد بود.
اگر میتوانید علت درستی این ادعا را توضیح دهید، در قسمت نظرات کامنت بگذارید.
رابطهای که در شکل نمایش داده شده صورتی تغییر یافته از تابع گاماست. تابع گاما (Γ) تعمیمی از تابع فاکتوریل برای اعداد حقیقی و مختلط (بجز اعداد صحیح منفی) بدست میدهد.
تعمیم تعریف فاکتوریل (1x2x3x...xN) به خارج از مجموعه اعداد طبیعی از قرن ۱۷هم مورد توجه ریاضیدانانی مثل برنولی بوده است. با وجود اینکه تابع گاما کاربرد مشخصی ندارد تحقیقات نظری مفصلی در مورد آن انجام شده است و مهمترین دلیل آن همین خاصیت تابع گاماست. برای دیدن بعضی از این نتایج ویکی پدیا را ببینید.
همچنین در قسمت نظرات تصاویر بیشتری را راجع به تابع گاما مشاهده کنید.
بردار های ویژه و مقادیر ویژه ماتریس کاربرد وسیعی در علوم مهندسی و ریاضیات کاربردی دارند.
اگر ماتریس مربعی A به ابعاد nxn را در بردار n بُعدی u ضرب کنیم، حاصل این ضرب بردار n بعدی v میشود: Au=v
اگر v در امتداد u واقع شود u بردار ویژه ماتریس است، یعنی Au=lamda*uکه در این صورت lamda مقدار ویژه متناظر با بردار ویژه u است. اهمیت رابطه فوق در این است که یک عدد جایگزین ماتریس شده است.
بردار ویژه در واقع فقط یک امتداد است. یعنی اگر u بردار ویژه باشد، a*u نیز بردار ویژه است که a میتواند 1- نیز باشد. هر ماتریس nxn اگر دترمینان آن صفر نباشد، n بردار ویژه دارد و اگر ماتریس متقارن باشد همه lamda ها و u ها حقیقی اند. یافتن مقادیر ویژه و بردار های ویژه ماتریس های با n>2 مستلزم حل معادله درجه n است که برای n های بزرگ کاری بسیار دشوار است. روشهایی برای یافتن بردارهای ویژه ابداع شده است که ساده ترین آنها Power Iteration است. این روش فقط بردار ویژه متناظر با بزرگترین lamda را می یابد ولی فرایند بسیار ساده ای دارد:
1. یک بردار تصادفیx0 را برداشته و ماتریس را در آن ضرب کنید: x1=Ax0
2. بردار حاصل را بر طول خودش تقسیم کرده تا بردار واحد شود.3. ماتریس را در بردار واحد حاصل ضرب کنید و عملیات مرحله های 2 و 3 را تکرار کنید تا زمانی که بردار حاصل هم جهت با بردار مضروب شود.
4. بردار حاصل بردار ویژه است و طول آن قبل از آنکه واحد شود برابر با قدر مطلق lamda است.
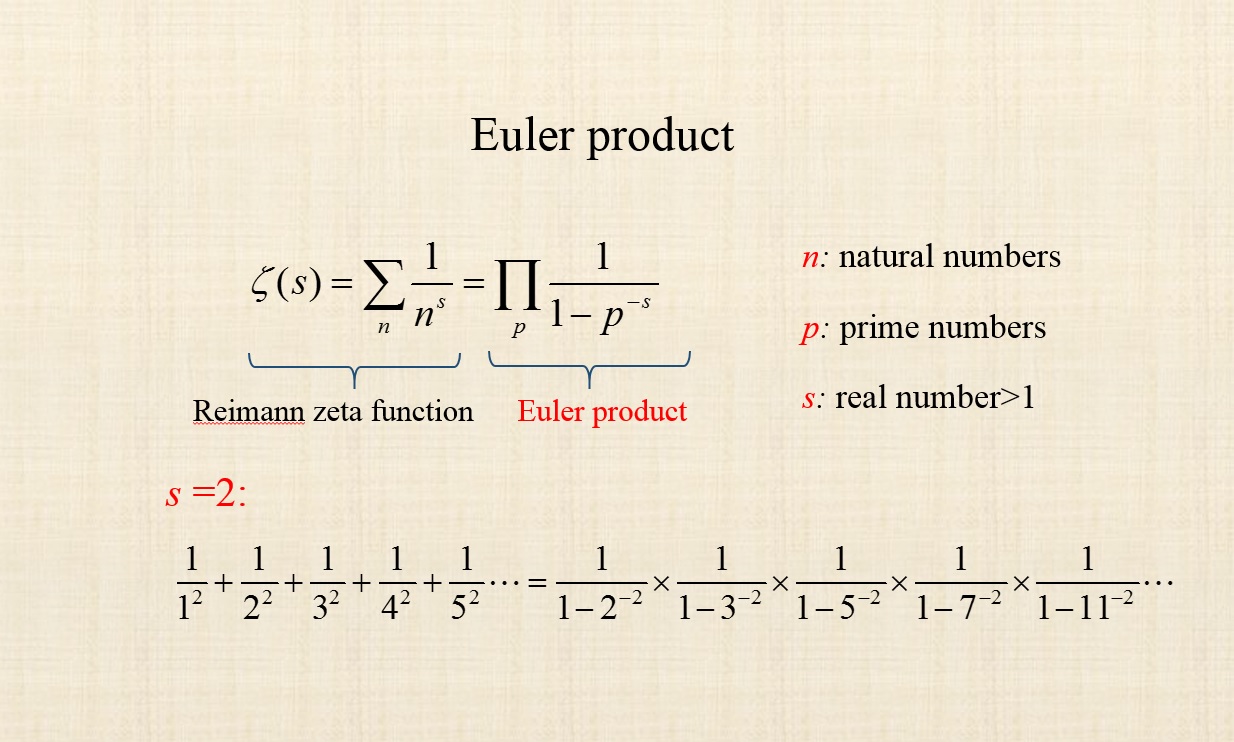
همانطور که در شکل نشان داده شده است، حاصلضرب اویلر برابر با تابع زیتای ریمان است. شگفتی این برابری در این است که یک مجموع نامتناهی با یک حاصلضرب نامتناهی برابر شده است.
اثبات زیبای این برابری را میتوانید در این لینک ببینید.
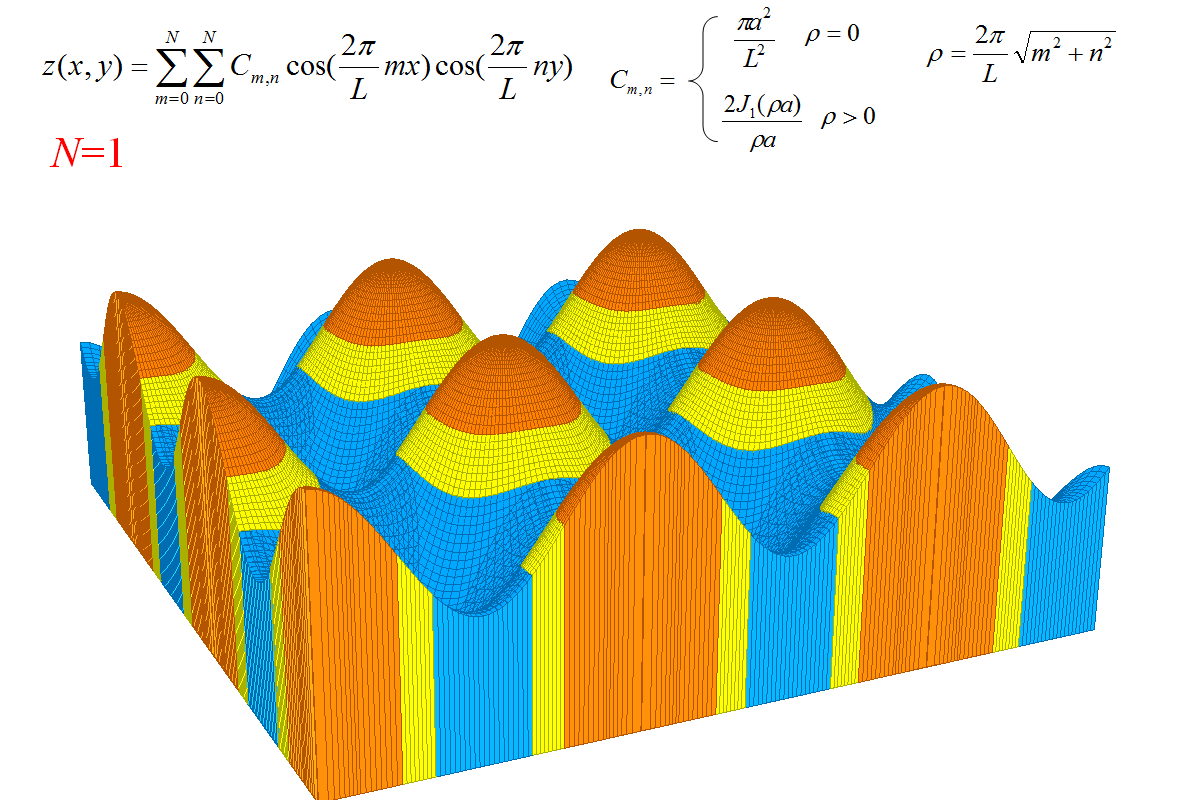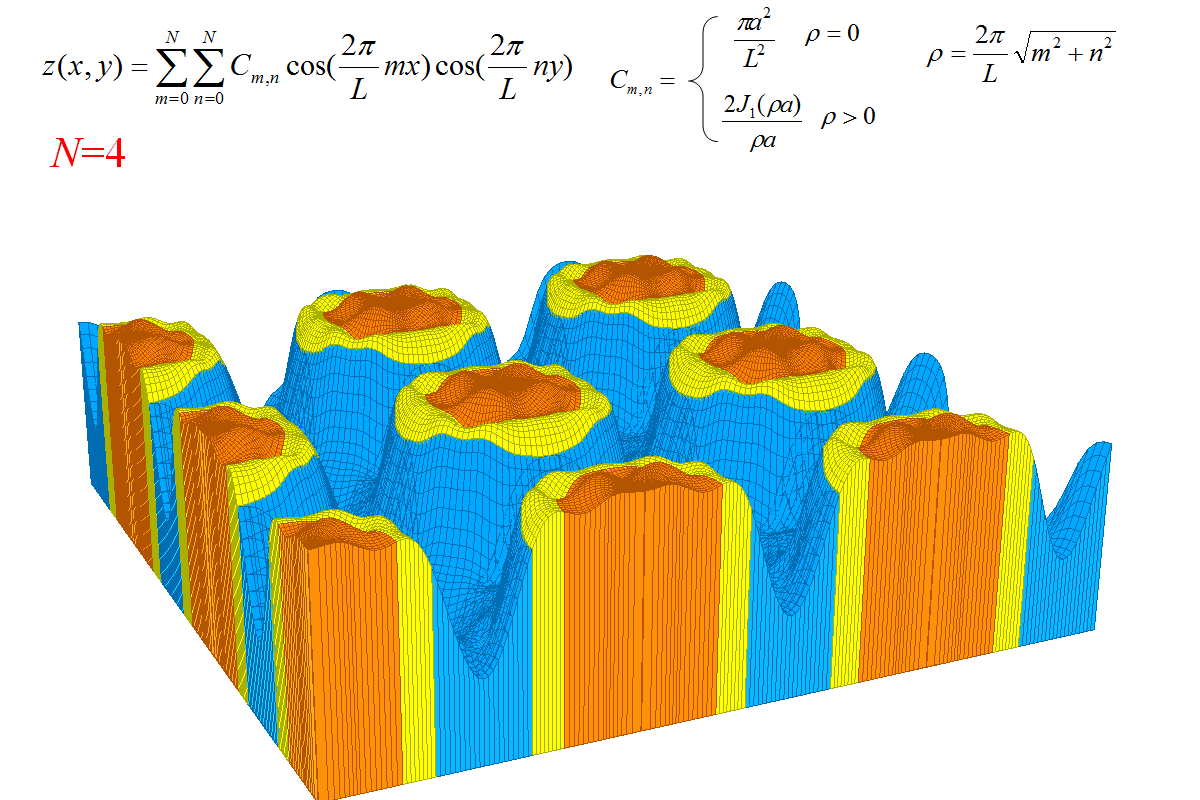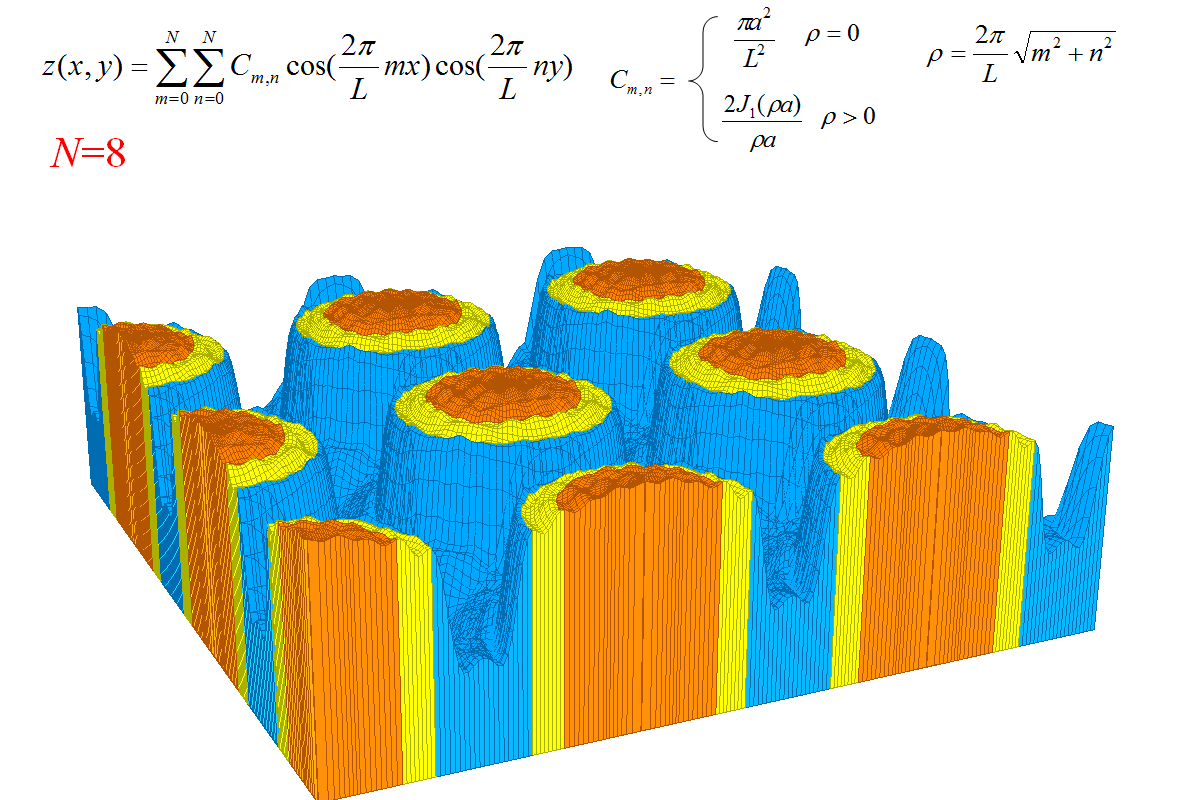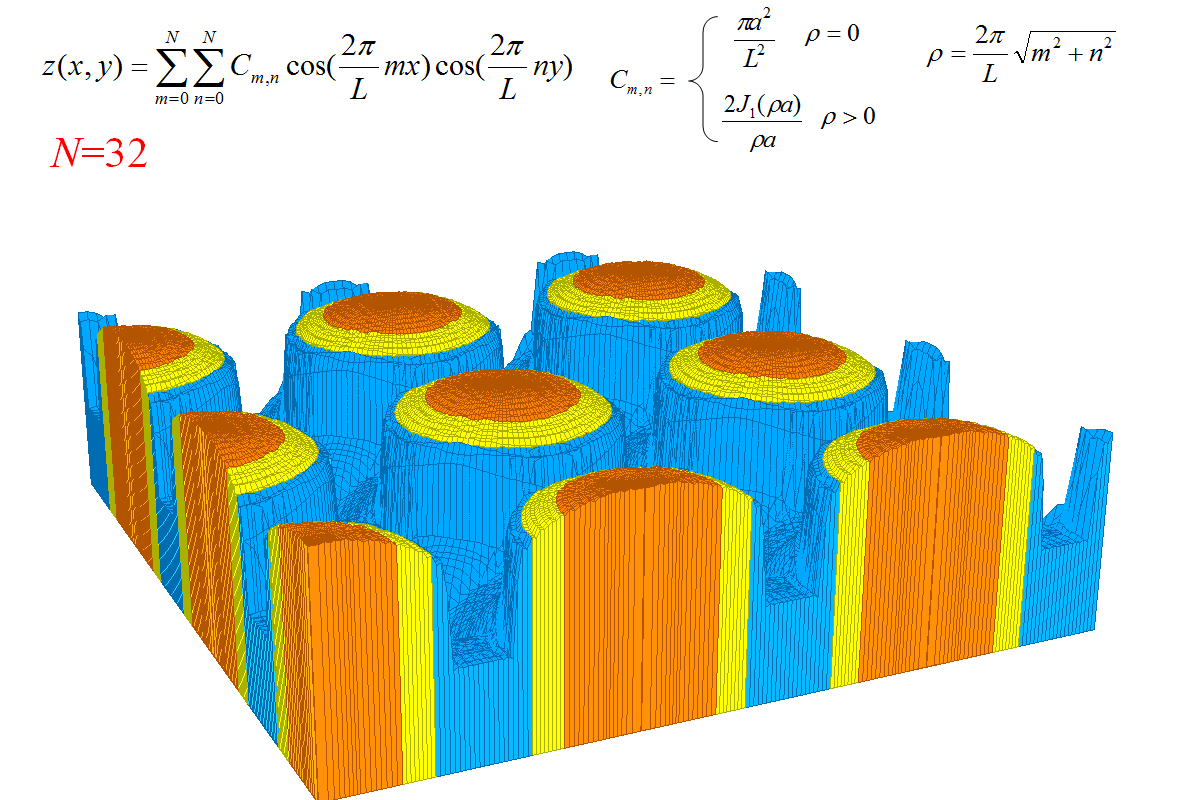
شکل هندسی زیبایی که سری فوریه نشان داده شده به آن همگرا میشود نتیجه یک اشتباه در محاسبات است. قصد داشتم استوانه را با سری فوریه دو بعدی بازسازی کنم ولی در نتیجه اشتباه در نوشتن بسط فوریه استوانه، این شکل که کمی با استوانه متفاوت است بدست آمد. سقف استوانه ها اندکی انحنا دارد و در مقایسه با باز سازی صحیح استوانه، لبه های استوانه برآمدگی (پدیده گیبز) بسیار کمتری دارند.بازسازی صحیح را نیز انجام داده ام ولی این شکل از آن زیباتر است.
شکل بر اساس فرمول های درج شده بالای تصویر ساخته شده است اما آن فرمول ها با بسط فوریه استوانه کمی تفاوت دارد. در بسط فوریه صحیح، جملاتی که m یا n غیر صفر دارند باید در 2 ضرب شوند؛ یعنی جملاتی که در آن m و n اگر هر دو صفر باشند ضریب 1 میگیرند، اگر فقط یکی از آن دو غیر صفر باشند ضریب 2 و اگر هر دو غیر صفر باشند ضریب 4. در این شکل برای همه جملات ضرایب 1 بکار رفته است.
Frobenius norm ماتریس برابر است با جذر مجموع مربعات عناصر ماتریس.
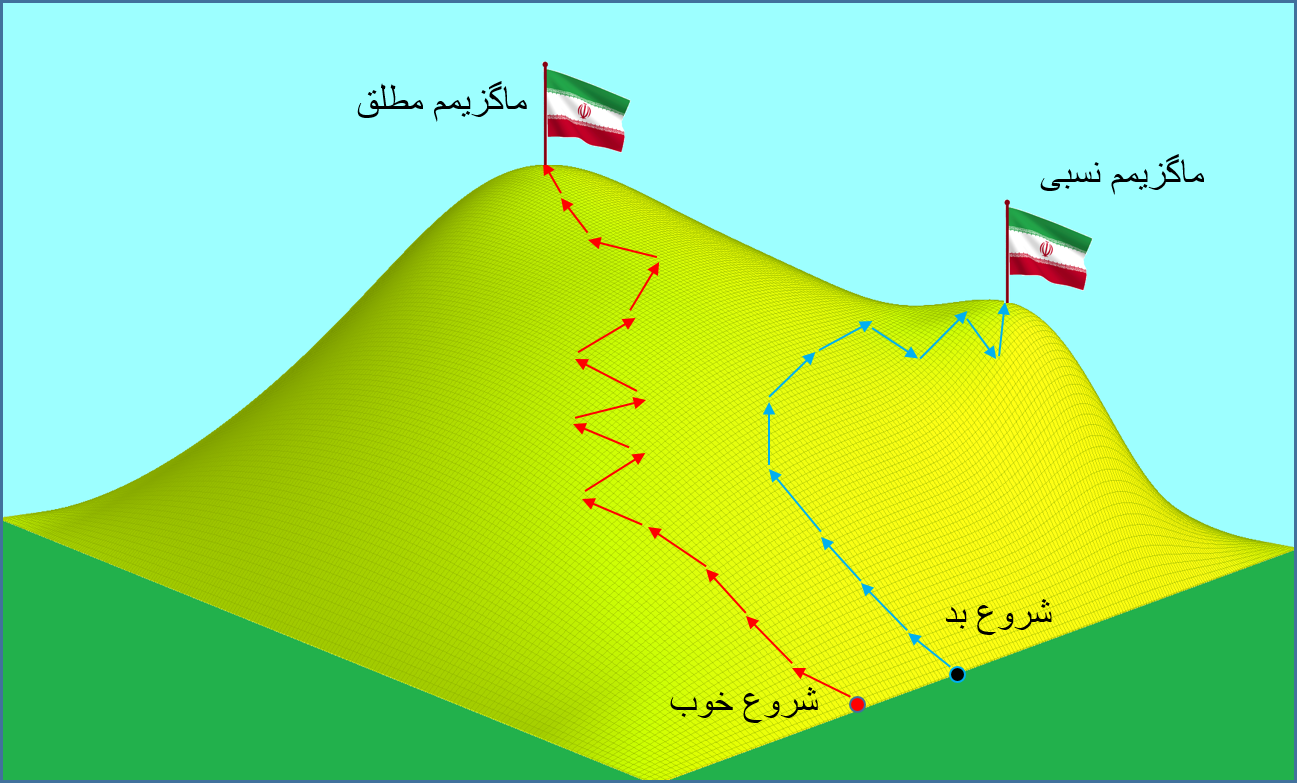
یکی از مسائل رایج در علوم مهندسی یافتن مقدار کمینه یا بیشنه توابع چند متغیره است که طبق معمول، این کار را نیز به کمک کامپیوتر انجام میدهند. یافتن مقدار بیشینه برای کامپیوتر مانند پیدا کردن قله تپه در هوای مه آلود است برای آدمی. کامپیوتر فقط تعریف تابع را داد و هیچ ایده ای در مورد موقیعت قله ندارد بلکه از یک نقطه حدسی شروع کرده و در جهت بیشترین شیب که همان بردار گرادیان تابع است مسافتی را طی کرده تا به نقطه جدیدی برسد. سپس و از آنجا دوباره بیشترین شیب را دنبال میکند و همینطور ادامه میدهد تا به قله برسد. اما در حالت کلی یافتن مسافت بهینه در هر مرحله کار دشواری است، از این رو معمولا روش ساده گام های کوچک را بکار میبرند. در این روش در هر مرحله مسافت کمی در جهت بردار گرادیان پیش رفته تا به نقطه جدید برسد. سپس در نقطه جدید مجددا بردار گرادیان محاسبه میشود و همینطور تا قله پیش میرود. این روش ساده هم معمولا به خوبی روش مسافت بهینه جواب میدهد اما ممکن است نیاز به محاسبه گرادیان به دفعات بسیار زیاد باشد.
بطور کلی الگوریتم دنبال کردن شیب gradient ascent نامیده میشود. یکی از مشکلات این الگوریتم و الگوریتم های مشابه این است که ممکن است، بستگی به نقطه شروع، به جای ماگزیمم مطلق، به ماگزیمم نسبی را پیدا کنند. در این نقطه بردار گرادیان صفر میشود و الگوریتم بر این گمان است که به قله رسیده است.
یافتن مقدار کمینه تابع کاملا مشابه همین الگوریتم است با این تفاوت که در هر مرحله باید در جهت عکس بردار گرادیان پیش رفت که در این حالت gradient descent نامیده میشود.
#ریاضیات_کاربردی
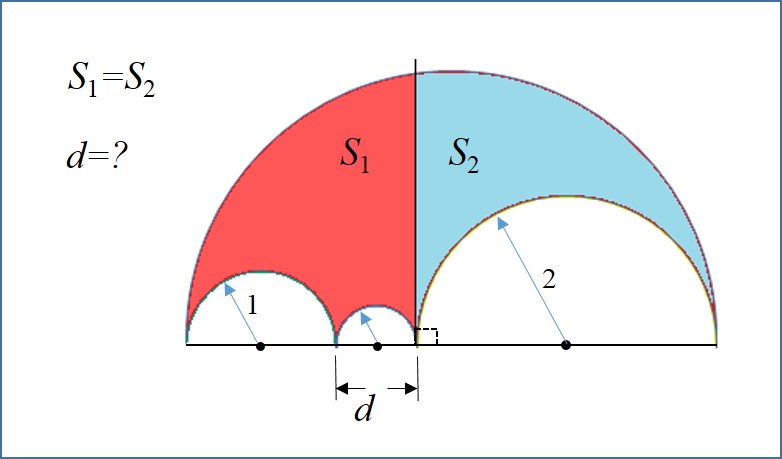
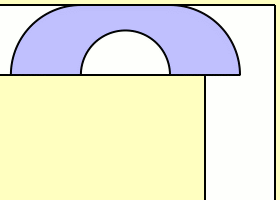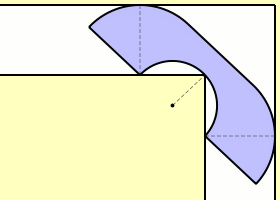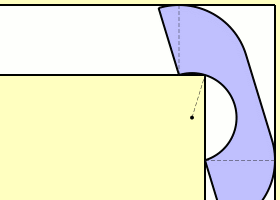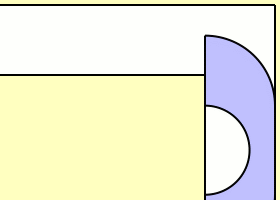
مساحت دو قسمت قرمز و آبی که در شکل مشخص شده اند با هم برابر و قوس ها همه نیم دایره اند. مقدار d را چقدر است.
برای اسباب کشی مجبورید کاناپه خود را از پیچ 90 درجه راهرو تنگی به عرض 1 متر بگذرانید. این را یک مساله را دو بعدی در نظر بگیرید و کاناپه را یک شکل دلخواه تصور کنید که میتواند هیچ شباهتی هم به کاناپه نداشته باشد. بزرگترین کاناپه ای که میتوان از پیچ راهرو گذراند چند متر مربع مساحت دارد؟
مساحت این کاناپه به ثابت کاناپه معروف است. ریاضیدانان هنوز مقدار دقیق این ثابت را نیافته اند ولی توانسته اند ثابت کنند که عددیست بین 2.2195 و 2.37.
درکارتون فوتبالیست ها، بارها شاهد صحنه هایی بوده ایم که با عبور کاپیتان سوباسا از خط وسط زمین و پیشروی او به سمت دروازه حریف، کم کم دروازه و دروازه بان از پشت انحنای کره زمین ظاهر میشوند.
به فرض اینکه طول زمین 90 متر و ارتفاع دروازه 2.44 متر است و دوربینی که صحنه را میبیند روی کفش کاپیتان سوباسا نصب شده است، شعاع کره زمین چند متر است؟
حافظه مورد نیاز را که محاسبه کنید جواب سوال معلوم میشود. حتی اگر حافظه کافی برای ذخیره ماتریس موجود باشد، زمان مورد نیاز برای حل دستگاه، عددی نجومی خواهد شد.
اما معمولا چنین است که بیشتر عناصر ماتریس ضرایب صفر هستند و نیاز به ذخیره آنها نیست. گاهی چنین معادلاتی با چند میلیون مجهول را نیر میتوان روی کامپیوتر معمولی حل کرد.
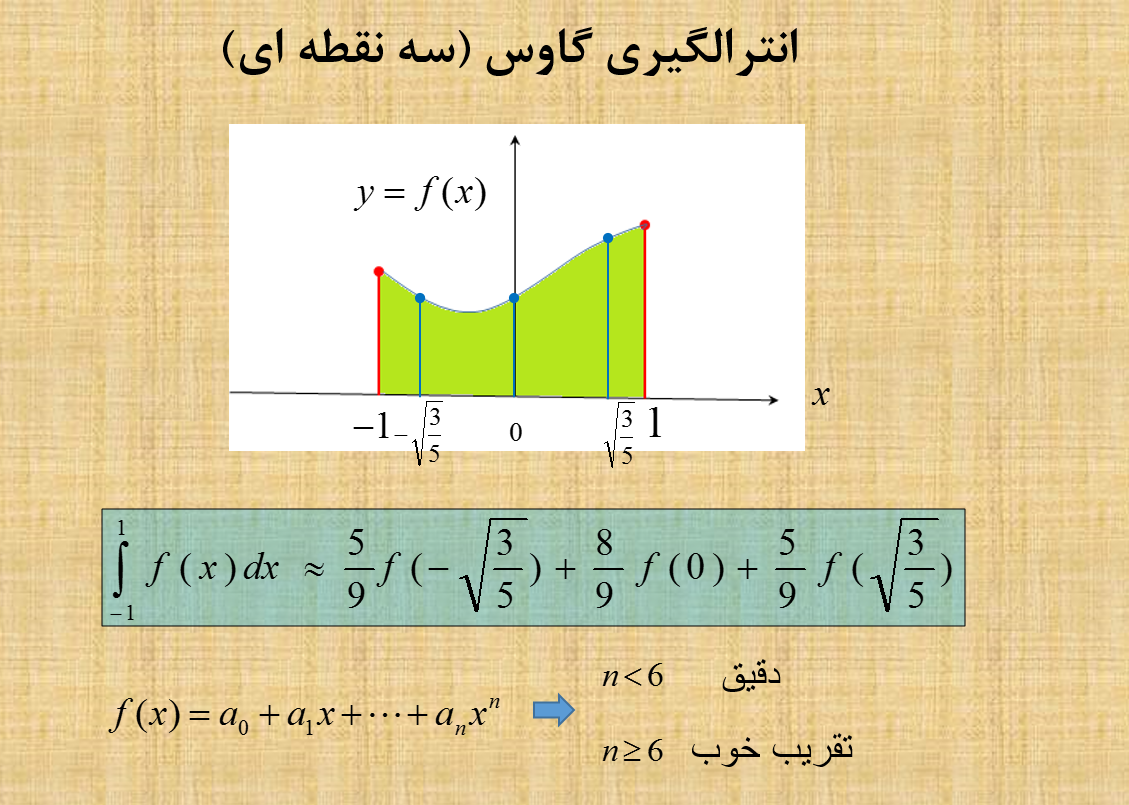
این روش انتگرالگیری کاربرد فراوان در نرم افزارهای محاسباتی اِلِمان محدود دارد. در شکل یک بعدی آن نشان داده شده است اما به ابعاد بالاتر قابل تعمیم است. برای انتگرال سه گانه بعدی 27 نقطه لازم است.
اثبات فرمول مشتقِ نسبت دو تابع، توسط اسحاق نیوتن، بنیانگذار علم حساب دیفرانسیال.
علامت «سه نقطه» به عنوان علامت نتیجه میدهد بکار رفته است.دانش آموزان امروزی این رابطه و اثبات ساده آن را در دبیرستان می آموزند، اما زمانی که نیوتون کتاب «روش فلاکسیون» را مینوشت، فقط او که بنیانگذار این حساب بود با مفهوم مشتق آشنا بود ( نیوتون اصطلاح فلاکسیون را برای مشتق بکار میبرد). این کتاب در سال 1671 تکمیل شد اما اولین چاپ رسمی آن حدود ده سال پس از مرگ نیوتون در سال 1736 صورت گرفت.