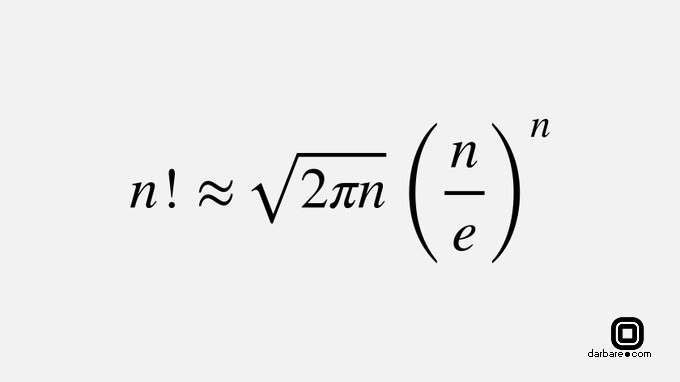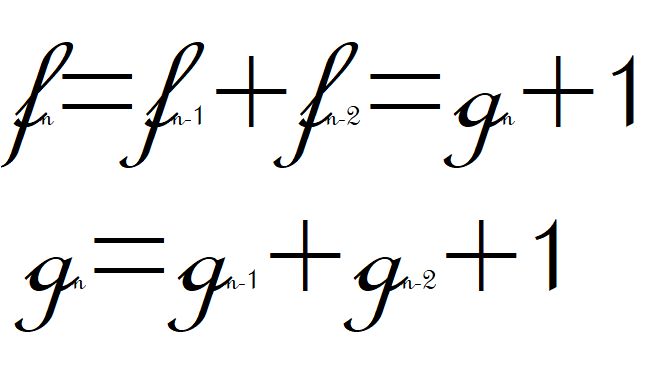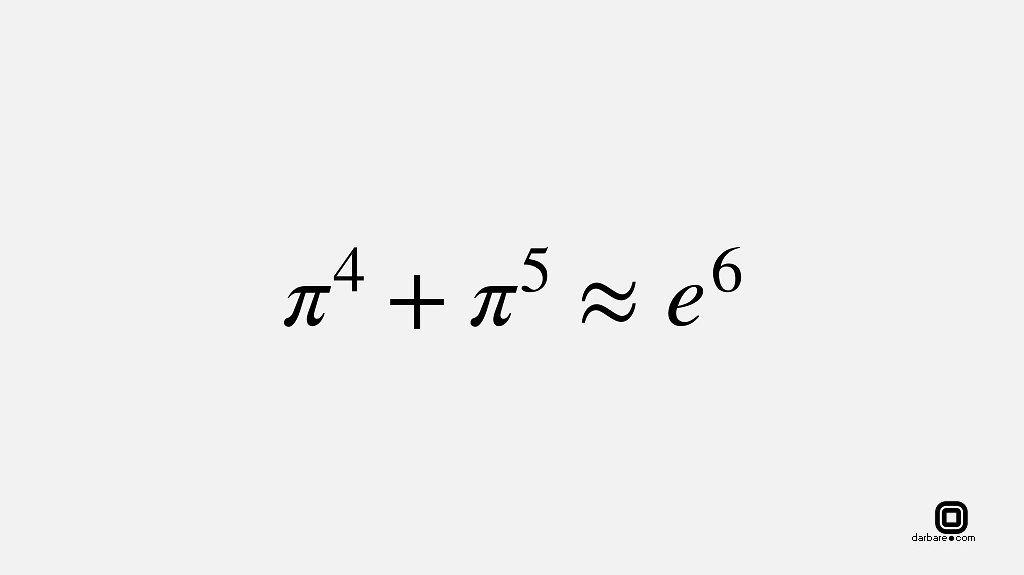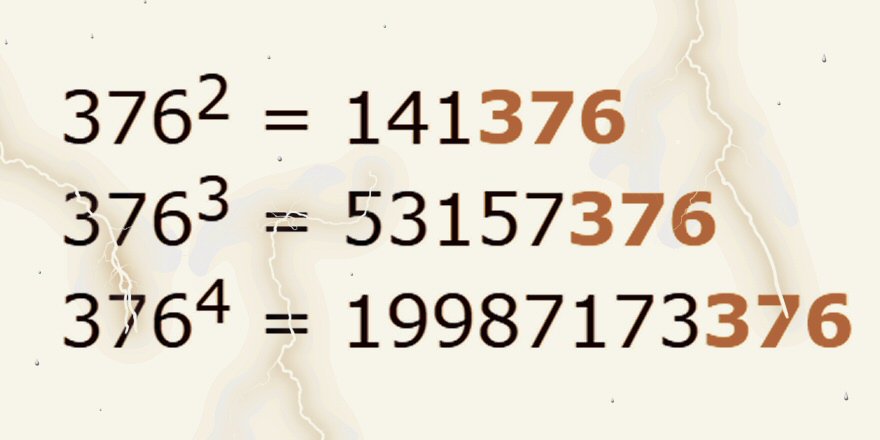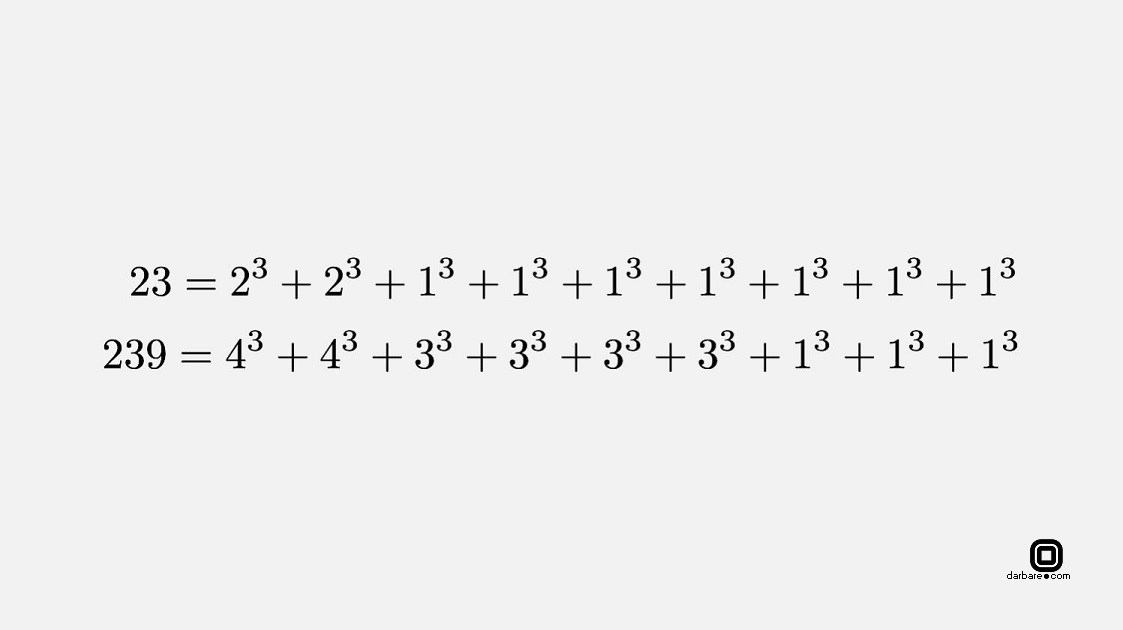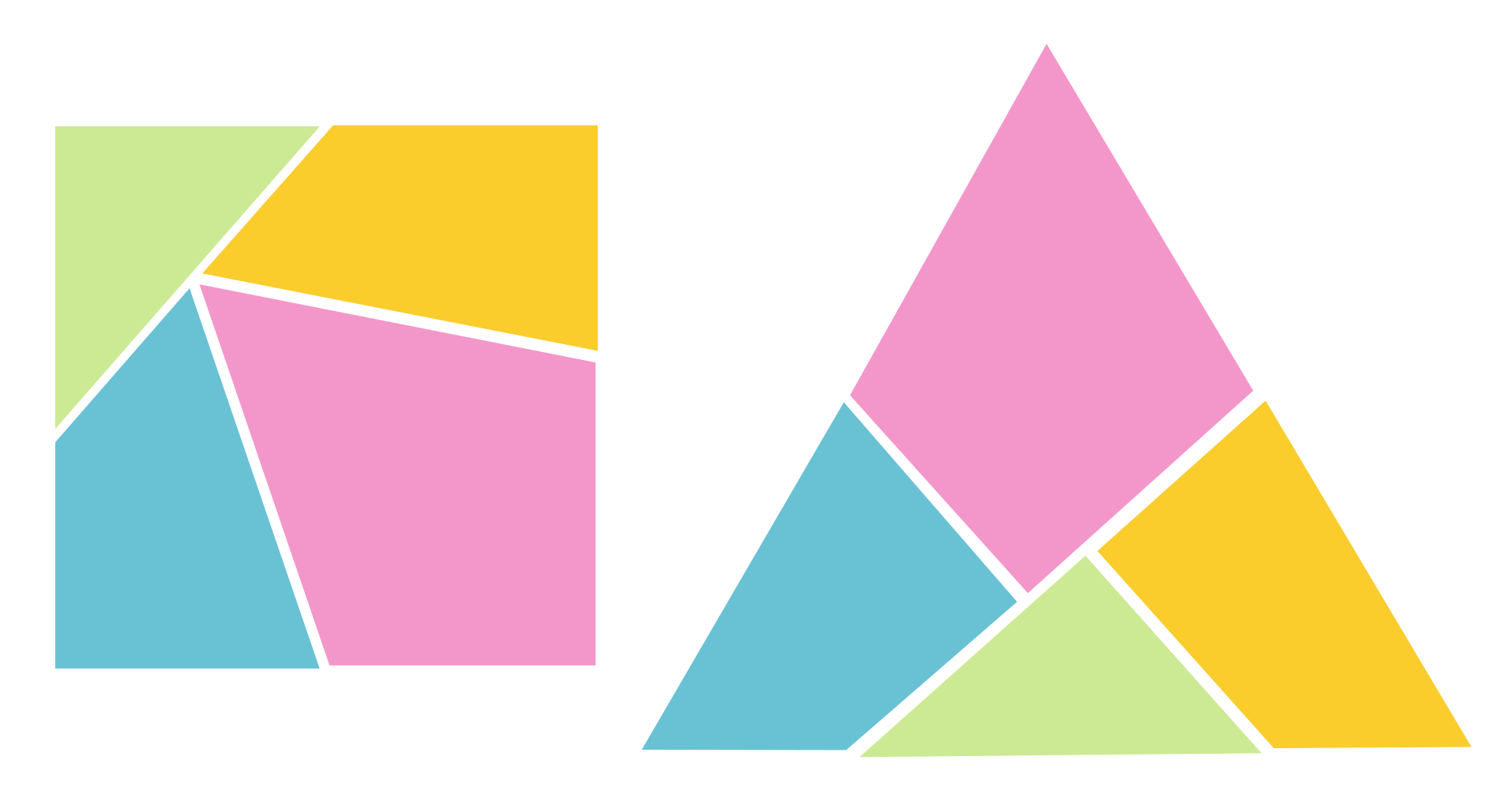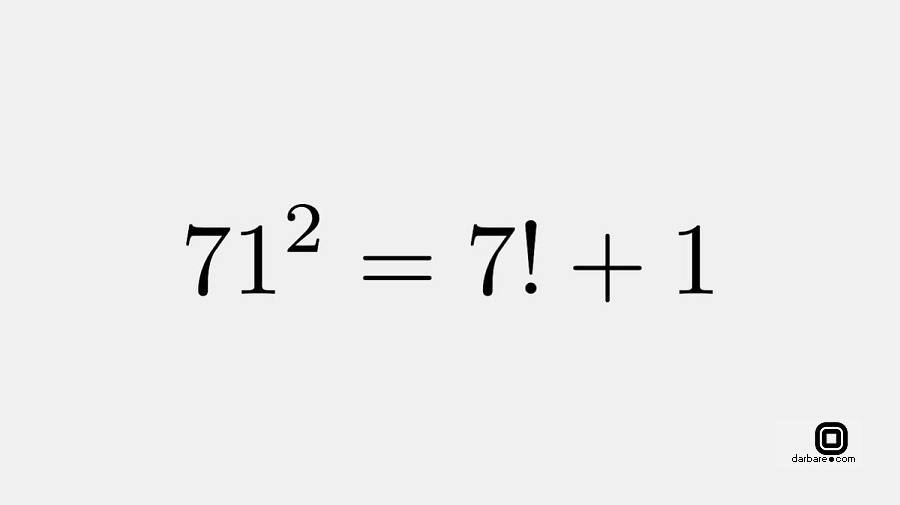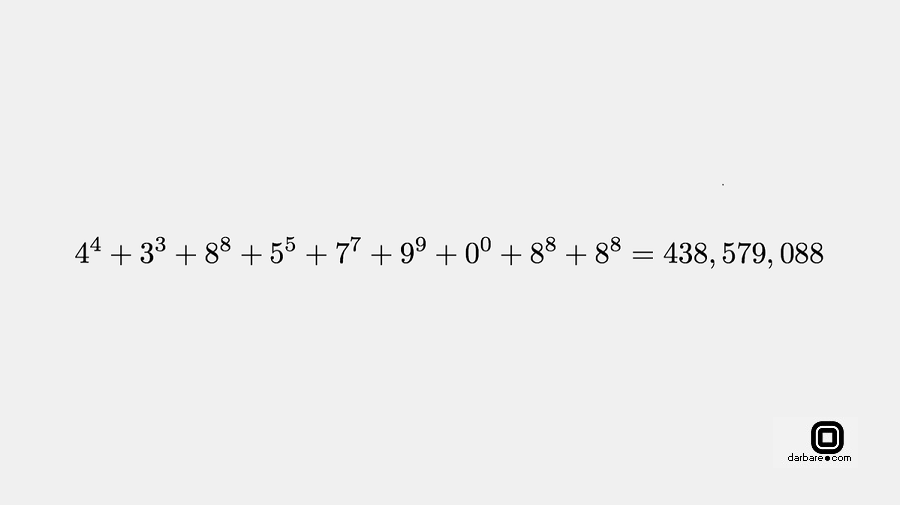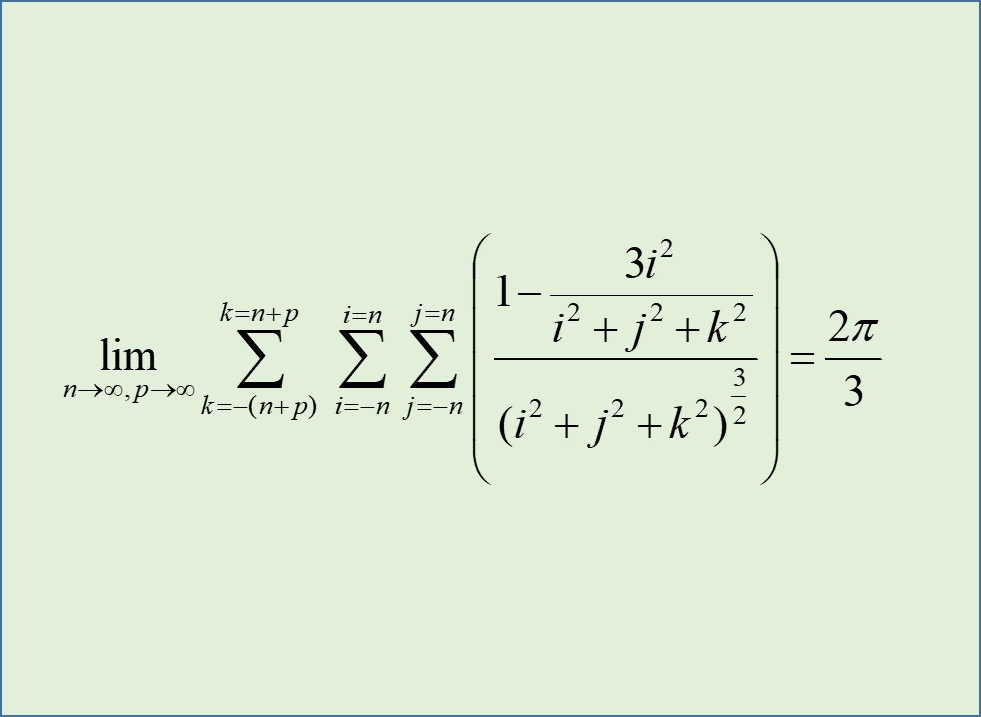#بلبل_زبان #شجریان #محمدرضا_شجریان
اگر موفق به اثبات این قضیه شدید راه حل را در قسمت نظرات به اشتراک بگذارید.
الگوی معروف 1و1و2و3و5و8و13و... را همه می شناسیم و به آن الگوی فیپوناچی می گویند و به صورت زیر تعریف می شود:
f(n)=f(n-1)+f(n-2) f(1)=1 f(2)=1
حالا من داداش کوچیکه ی فیپوناچی را به شما معرفی می کنم:
g(n)=g(n-1)+g(n-2) g(1)=g(2)=0
جمله های ابتدایی این الگو به صورت 0و0و1و2و4و7و12و... است و به راحتی
می توان نشان داد که همواره:
g(n)=f(n)-1
اگر موفق به یافتن نمونههای دیگری از این الگو شدید یا توانستید ادعای این پست را اثبات کنید مطلب را در قسمت نظرات به اشتراک بگذارید
همین الان با استفاده از یکی از ابزارهای آنلاین سعی کنید بزرگترین مقسوم علیه مشترک دو عدد n^17+9 و (n+1)^17+9 را به ازای مقادیر مختلف n محاسبه کنید. خواهید دید که این مقدار برابر یک خواهد بود. در حقیقت اگر با شروع از یک مقادیر n را با سرعت هزاران مقدار در ثانیه در رابطه بگذارید تا پایان عمر جهان نتیجه یک خواهد بود.
با این وجود این الگو برای همه مقادیر n درست نیست و در حقیقت اولین باری که مقسوم علیه مشترک این دو عدد غیر از یک خواهد بود به ازای مقدار زیر برای n میباشد:
8424432925592889329288197322308900672459420460792433
نتیجه اخلاقی: هیچ ادعایی در ریاضیات بدون اثبات قابل پذیرش نیست حتی اگر برای میلیونها مقدار درست باشد!
روشهای دیگری را که برای اثبات واگرایی این مجموع سراغ دارید در قسمت نظرات به اشتراک بگذارید.
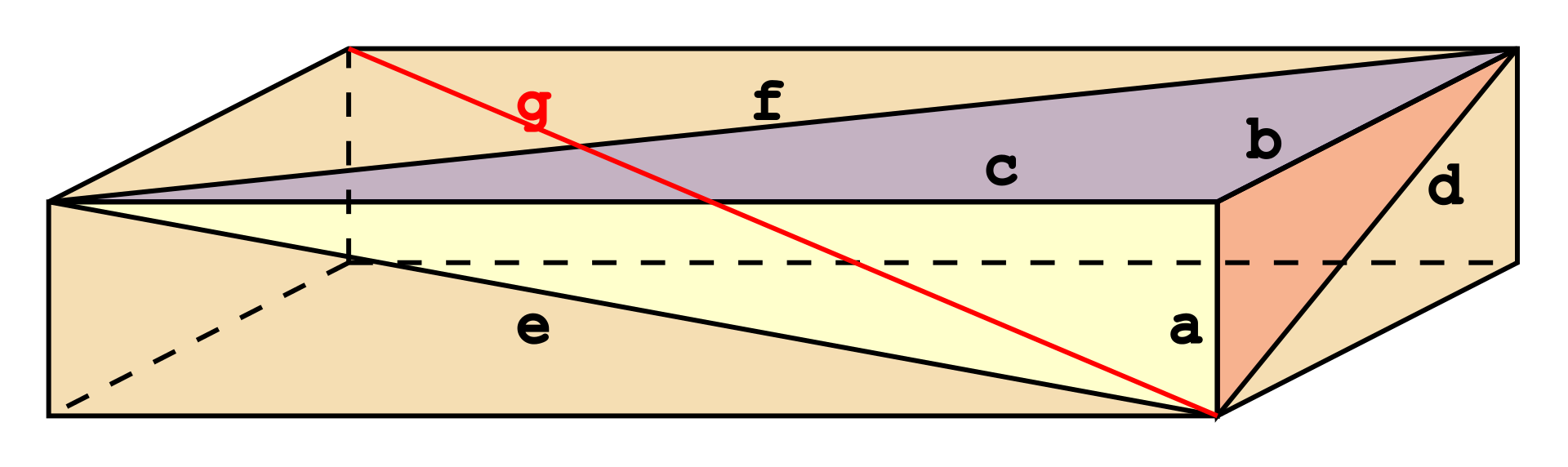
روی اضلاع شش ضلعی آبی رنگ مثلثهای متساوی الاضلاع قرمز و سپس زرد ساخته شدهاند. نشان دهید وسط خطوطی که مراکز مثلثهای روبرو را به هم وصل میکنند راسهای دو مثلث متساویالاضلاع دیگر هستند.
ضمنا رئوس مثلث قرمز رنگ کوچک روی وسط اضلاع مثلث دیگر قرار دارد.
به نظر شما آیااین الگو با ساخت مثلثهای جدید روی نقاط C ادامه مییابد؟
آیا این الگو یا الگوی مشابه برای هشت ضلعی یا مربع هم وجود دارد؟
در ریاضیات، آجر اویلر یا مکعب اویلر که بهنام لئونارد اویلر نامگذاری شده است، مکعبی است که لبهها و تمامی قطرهای آن اعدادی طبیعی هستند. آجر اصلی اویلر نیز به مکعبی گفته میشود که طولهای آن نسبت به هم اول باشند.
ابعاد یک آجر اویلر را میتوان مطابق با پاسخ معادله سیاله زیر در نظر گرفت.
در رابطه فوق a,b,c برابر با طول لبهها بوده و d,e,f نشاندهنده قطرها هستند. این مکعبها ویژگیهایی خاص داشته از این رو از آن در علوم و مهندسی استفاده میشود.
کوچکترین آجر اویلر در سال ۱۷۱۹ توسط «پاول هالک» (Paul Halcke) بدست آمد. لبههای این آجر برابر است با:
(d,e,f ) = (125, 244, 267)
در ادامه برخی دیگر از مهمترین ابعاد یافته شده به عنوان آجر اویلر نیز ارائه شدهاند.
(85,132,720) — (157,725,732)
(140,480,693) — (500,707,843)
(160,231,792) — (281,808,825)
(187,1020,1584) — (1037,1595,1884)
(195,748,6336) — (773,6339,6380)
(240,252,275) — (348,365,373)
(429,880,2340) — (979,2379,2500)
(495,4888,8160) — (4913,8175,9512)
(528,5796,6325) — (5820,6347,8579)
آجر کامل
یک آجر کامل، مکعبی اویلری محسوب میشود که قطر فضایی آن نیز عددی صحیح است. به عبارتی دیگر معادله زیر نیز باید بین ابعاد اصلی (یا همان لبهها) برقرار باشد. قطر فضایی، قطری است که دو گوشه مخالف مکعب را به هم وصل میکند.
در رابطه فوق g نشاندهنده قطر فضایی است. تاکنون کسی مکعبی کامل را پیدا نکرده و هیچکس نیز هنوز وجود نداشتن مکعب کامل را اثبات نکرده است.
آجر اصلی کامل یا آجر اولیه کامل نیز به مکعبی گفته میشود که هم لبهها و قطرهای وجوه آن، اعدادی صحیح بوده و همزمان نسبت به هم اعدادی اول باشند.
آجر تقریبا کامل
یک مکعب تقریبا کامل، از 7 طول، دارای 6 طول صحیح است. چنین مکعبهایی را میتوان در سه دسته حجمی، طولی یا سطحی تقسیمبندی کرد. در مورد مکعب حجمی، طول قطر فضایی عددی گنگ است. در مکعب طولی نیز یکی از لبههای a،b،c عددی گنگ خواهد بود.
نویسنده:سجاد اسدی
در ریاضیات به یک عدد زمانی عدد شگفت انگیز گفته میشود که n رقم آخر مربع عدد، برابر با خود عدد باشد. برای مثال 625 = 25*25 و 5776 = 76*76. این اعداد به نام اعداد اتومورفیک نیز نامیده میشوند.
اعداد اتومورفیک بزرگتری مانند 212890625 و 787109376 نیز وجود دارند:
2128906252 = 45322418212890625
و
7871093762 = 619541169787109376
همچنین باید بدانید که اگر n رقم آخر مربع عدد برابر با خود عدد باشد، این رابطه در مورد مکعب عدد و توانهای بالاتر نیز صدق میکند. مشخص شده است که برای هر n>1 دو عدد شگفت انگیز به طول n وجود دارد.
حتی یک فرمول نیز برای این دو عدد وجود دارد. فرمول نخست به صورت باقیمانده 5 به توان 2n تقسیم بر 10nاست و دومی به صورت 10n + 1 منهای اولی است.
نویسنده:سجاد اسدی
جالب اینجاست که در این بین ۲۳۹ و ۲۳ تنها دو عددی هستند که ۹ مکعب لازم دارند و سایر اعداد با یک تا هشت مکعب کامل قابل بازسازی هستند.
در حالت کلی برای هر عدد طبیعی n یک عدد طبیعی s وجود دارد بطوریکه میتوان همه اعداد طبیعی را بصورت مجموع حداکثر s توان n ام نوشت. برای مثال هر عدد طبیعی را میتوان بصورت مجموع حداکثر ۱۹ توان چهارم نوشت. درستی این قضیه که به مسئله وارینگ مشهور ۱۴۰ سال بعد از مطرح شدن آن در سال ۱۹۰۹ توسط هیلبرت به اثبات رسیده است. در ویکیپدیا راجع به آن بیشتر بدانید.
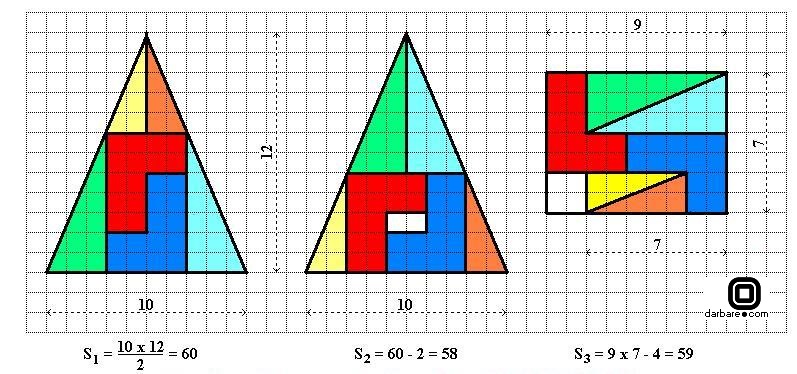
همواره میتوان با تعداد محدودی برش ساده قسمتهای یک چندضلعی دلخواه رو طوری بازچینی کرد که چندضلعی دلخواه دیگری با مساحت برابر را بپوشاند. این قضیه صرف نظر از شکل چند ضلعیها و محدب یا مقعر بودن آنها صحیح است. اثبات این ادعا چندان مشکل نیست و در سال ۱۸۰۷ برای اولین بار به انجام رسیده است.
برای دانستن بیشتر در مورد این مسئله ویکیپدیا را ببینید.
هیلبرت ریاضی دان معروف که در زمان حیاتش فهرستی از مهمترین مسایل ریاضی حل نشده را منتشر کرد در سومین مسئله این سوال را مطرح کرد که آیا معادل این مسئله در فضای سه بعدی برای چندوجهیهایی با حجم برابر هم درست است یا نه. به عبارت دیگر آیا میتوان با تعداد محدودی برش مستقیم و جابجایی و چرخش قطعات یک چند وجهی را (مثلا یک هرم) به یک چند وجهی دیگر (مثلا یک مکعب) با حجم برابر تبدیل کرد. دوسال بعد و در زمان حیات هیلبرت یکی از شاگردانش نشان داد که این موضوع همواره امکانپذیر نیست. در ویکیپدیا بیشتر بخوانید.
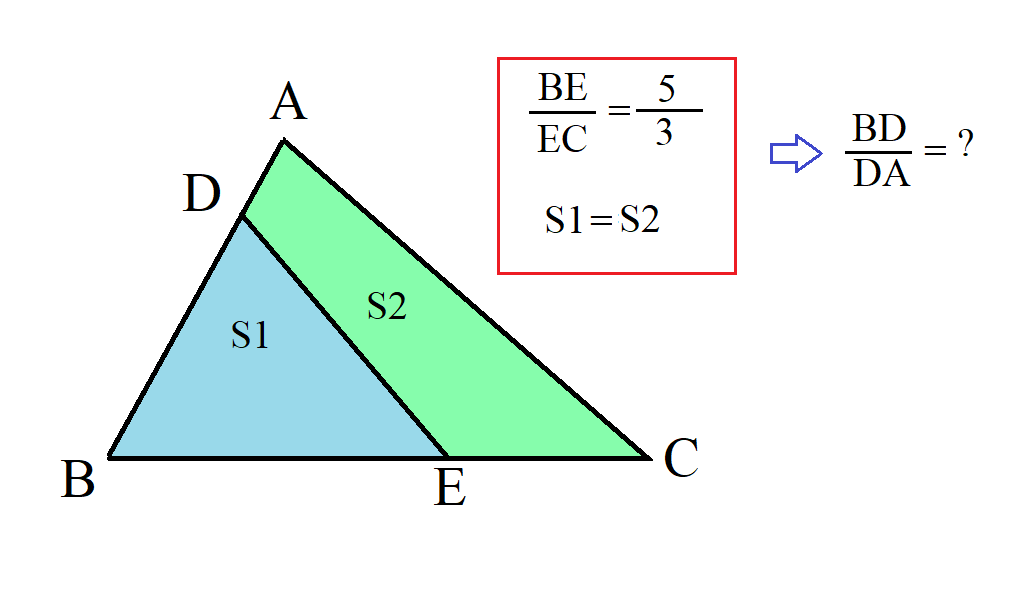
این سوال جالب و نسبتا ساده را در یک کتاب آمادگی آزمون ورودی یکی از مدارس راهنمایی خصوصی دیدم، یعنی دانش آموز کلاس ششم باید این را جواب بدهد. فکر میکنم برای دانش آموزان متوسط و حتی خوب سخت است.
مسئله بروکارد یافتن پاسخهای معادله !m*m = 1 + n در مجموعه اعداد طبیعی است. این مسئله در سال ۱۸۷۶ برای اولین بار مطرح شد. تاکنون سه جواب برای این معادله پیدا شده است و حدس زده میشود جواب دیگری وجود ندارد.
درباره این مسئله و جوابهای دیگر آن ویکیپدیا را ببینید.
البته عبارت صفر به توان صفر در این رابطه یک فرض شده که فرضی نادرست است و با کنار گذاشتن آن فقط ۳۴۳۵ و یک دارای این خاصیت هستند. اگر موفق به اثبات این ادعا شدید راه حل خود را در قسمت نظرات به اشتراک بگذارید.
چند وقت پیش در حین انجام محاسباتی به این سری رسیدم. آن را جایی ندیده ام و میتوانم بگویم اوریجینال است، ولی یقین دارم ریاضی دانها و یا حد اقل فیزیکدانها با مفهوم آن آشنایند هر چند ممکن است به این صورت مطرح نکرده باشند. از آنجا که سری شامل سه مجموع است با دو حد بی نهایت است، اثبات ریاضی آن شاید دشوار باشد ولی با استفاده از قوانین الکترو مغناطیس نسبتا به راحتی اثبات میشود.